Saturn

The devil is in the details.

0%

Notes of CRaft

Posted on Edited on In

Raft协议

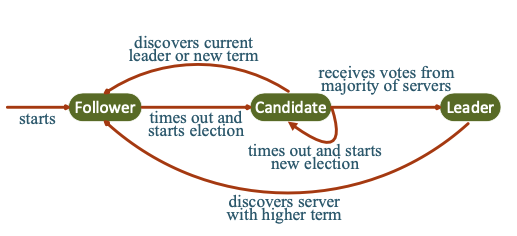
image-20230316131248161

流程：

  1. 选主，投票，确认
  2. 向Leader发送日志
  3. Leader分发日志，F+1个slave确认
  4. Leader提交日志，回复client，同步commit信息

Raft协议保证两个properties：

  1. Safety. They never return incorrect results under all non- Byzantine conditions.
  2. Liveness. They are fully functional as long as any majority of the servers are alive and can communicate with each other and with clients. We call this group of servers healthy.

Safety property由Leader Completeness Property 保证： if a log entry is committed in a given term, then that entry will be present in the logs of the leaders for all higher-numbered terms.

Liveness 由Raft的rule保证。

Erasure Coding

纠删码是一种通用的用来在存储和网络传输领域容错的手段。

Reed-Solomon code（RS-code）

原理：

给定n个数据块d1, d2,…, dn，n和一个正整数m， RS根据n个数据块生成m个校验块， c1, c2,…, cm。 对于任意的n和m， 从n个原始数据块和m 个校验块中任取n块就能解码出原始数据， 即RS最多容忍m个数据块或者校验块同时丢失（纠删码只能容忍数据丢失，无法容忍数据篡改，纠删码正是得名与此）。

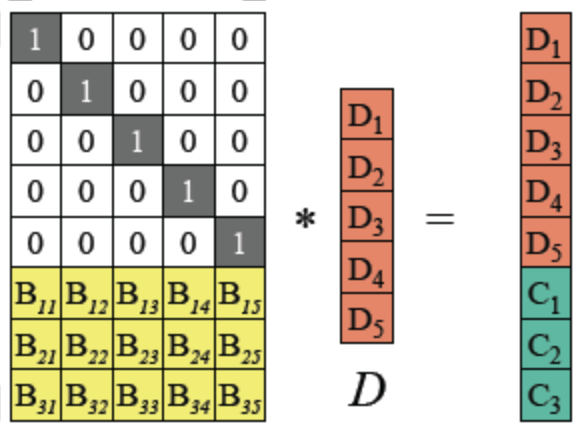
image-20230316132947759
单位矩阵：

定义：在线性代数中，nn阶单位矩阵，是一个n×nn\times n的方形矩阵，其主对角线元素为1，其馀元素为0。

性质：AI_{n}=A且InB=BI_{n}B=B(任何矩阵与单位矩阵相乘都等于本身)

范德蒙矩阵（vandermonde matrix）：

定义：{\displaystyle V={\begin{bmatrix}1&\alpha _{1}&\alpha _{1}^{2}&\dots &\alpha _{1}^{n-1}\\1&\alpha _{2}&\alpha _{2}^{2}&\dots &\alpha _{2}^{n-1}\\1&\alpha _{3}&\alpha _{3}^{2}&\dots &\alpha _{3}^{n-1}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&\alpha _{m}&\alpha _{m}^{2}&\dots &\alpha _{m}^{n-1}\\\end{bmatrix}}}

之所以采用vandermonde矩阵的原因是， RS数据恢复算法要求编码矩阵任意n*n子矩阵可逆。

逆矩阵：

性质：矩阵和其逆矩阵相乘，结果等于单位矩阵。

举例：

假设D1，D4和C2丢失，如何通过RS-code恢复？

  1. 根据编码的等式，获得B‘等式：
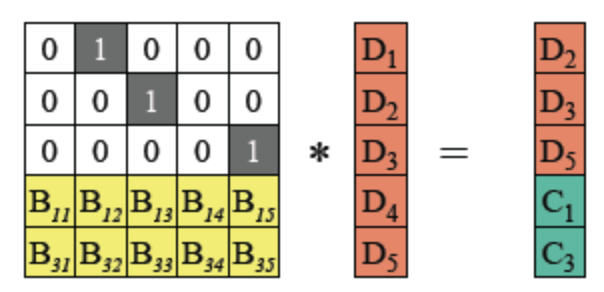
image-20230316134304214

  1. 由于编码矩阵可逆，将等式两边乘以编码矩阵的逆矩阵：

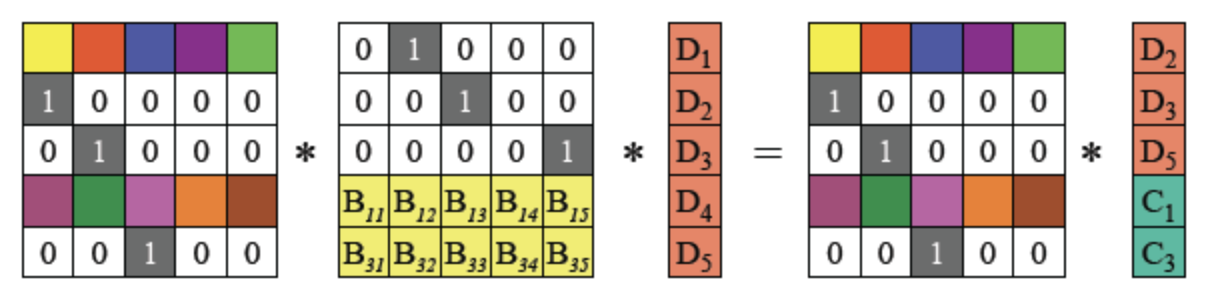
    image-20230316134640443

  2. 根据上面提到的逆矩阵性质，矩阵乘以其逆矩阵等于单位矩阵，得到以下等式

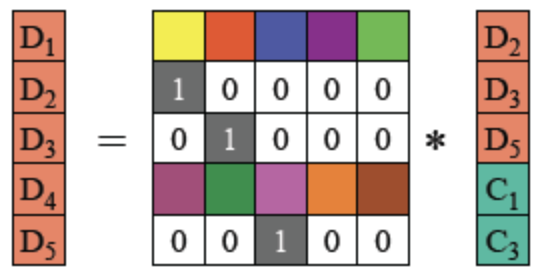
    image-20230316134737115

  3. 所以对幸存的fragment使用编码矩阵的逆矩阵进行重新编码，可以获取到原始的fragment。

此论文中RS-code的一些相关定义：

RS可以定义一组整数，k和m，data被等分为k组，使用k组fragment编码生成m组parity fragment，因此一共有k+m组编码后的fragment，称作coded-fragment。集群中有N个Server，每个Server存储一个coded-fragment，因此k+m = N。

RS-Paxos

RS-Paxos也是结合了RS纠删码，可以将存储代价大大降低，付出的代价是Liveness性质不能和Paxos一致。

假设集群中有2F + 1个节点，Paxos可以容忍F个节点的failure，因此将Liveness定义为F。Paxos算法和Raft算法都遵循排容原理（inclusion-exclusion principle）：

|A ∪ B| = | A |+| B |−| A ∩ B | (1)

（1）中是两个集合之间的排容原理：

  1. 假设有限集A和B不相交，则 A U B = A + B
  2. 假设有限集A和B相交，则A + B中交集算了两次，需要减去一次交集A ∩ B

inclusion-exclusion principle 保证了在一个Raft group中，两个majority必定至少有一个共同的节点。

证明：If |A| > |A∪B|/2 and |B| > |A∪B|/2, |A∩B| = |A|+|B|−|A∪B| > 0.

结论：RS-Paxos的Liveness是小于F的。

证明：

  1. RS-Paxos中，需要满足条件Qr + Qw − N ≥ k (2)：Qr和Qw的交集中的Server个数至少为k
  2. RS-Paxos中，至少要max(Qr,Qw)个healthy节点存在才能work
  3. 如果一个command被提交，那么至少Qw个节点accept过
  4. 如果某节点proposal一个command，那么在prepare阶段至少需要contact Qr个节点
  5. 设RS-Paxos的Liveness为L
1
2
3
1. L <= N - max(Qr,Qw)
2. 根据（2），max(Qr,Qw) >= (Qr + Qw)/2 >= (N + k)/2 
3. 根据以上两条，所以 L <= N - (N + k)/2 = (N - k)/2 = (2F + 1 - k)/2 = F - (k + 1)/2 < F

CRaft

设计目标：

  1. 提供和经典Raft算法一致的Liveness性质（通过限制1来实现）
  2. 通过RS-code,降低存储代价

限制：

  1. 在一个有2F+1个节点的Raft Group中，当只有F+1个节点存活时，log entry只有在被完整的复制到所有的F+1个healthy节点上后，才能被提交。

    证明：假设在2F+1个节点的Group中，当前时刻T1只有F+1个Server存活（S和剩余节点），有节点S和log e，e已经提交，S只存储了e的一个fragment。下一时刻T2，S存活，上一时刻的剩余节点全部unhealthy，上一时刻unhealthy的节点全部转为active，此时只有S存储有log e的一个fragment，无法恢复出完整的log，得证。

coded-fragment replication and complete-entry replication

Coded-fragment Replication

流程：

  1. encode原始log，获取k+m个fragment

  2. leader分fragments

  3. 至少F+k个slave成功收到fragment并响应leader后，leader commit此log

  4. 通知slave commit此log

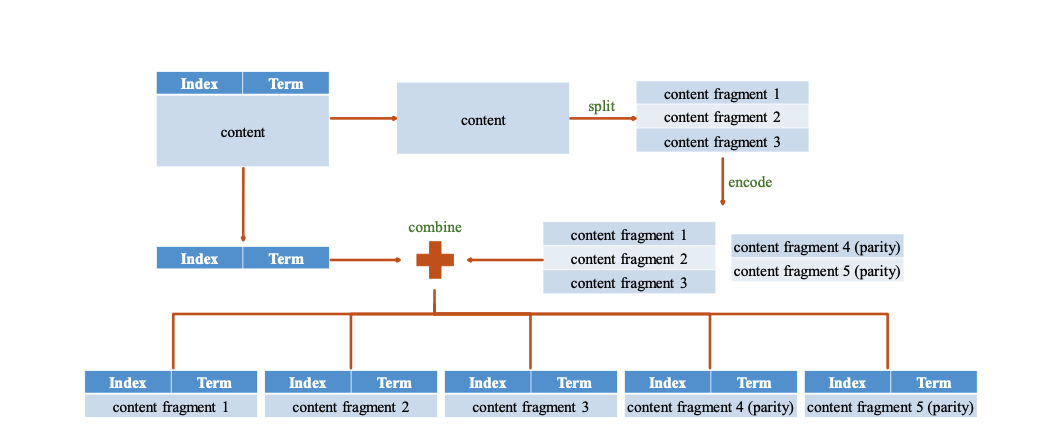
    image-20230316143621949

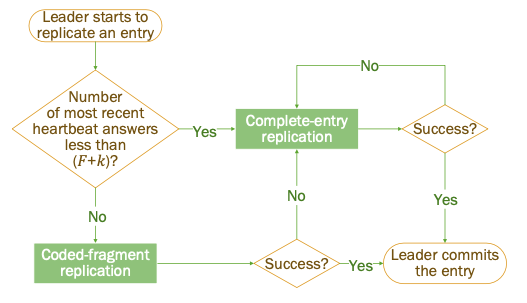
why F+k?

相较于经典raft理论中，leader在收到F+1个slave的成功响应后即可commit log，CRaft中的commit条件更为严格，在使用coded-fragment replication分发后，需要在F+k个slave响应后方能提交。F+k为了保证Liveness属性，保证了在leader选举后，leader能够正确的从fragment中恢复出完整的log entry。

证明：

假设T1时刻leader无响应，出发leader选举后，选举出新的leader。Raft的election rule保证了选举出的leader拥有最新最全的日志，假设日志e已经提交，新的leader必定拥有e的fragment，由于e已提交，因此至少F+k个Server存储了e的coded-fragments：

1
2
3
4
5
6
7
8
设 A = (F + k),B = (F + 1)
A + B = F + k + F + 1 = 2F + 1 + K
因为 2F + 1 = N
所以 A + B - N = 2F + 1 - N + K = k (1)
根据 A ∪ B = A + B − A ∩ B，因此 A ∩ B = A + B - A ∪ B (2)
由于 A 和 B都属于raft组的majority，因此 A ∪ B <= N
所以 A + B - N < A + B - A ∪ B，
带入 (1)和(2),的 k < A ∩ B

由以上推导可得，在Raft Group中任取F + 1个Server，这F + 1个Server中至少存在k个coded-fragments。

由于Rs-code要求至少要k个coded-fragments才能恢复数据，由此满足条件。

反例

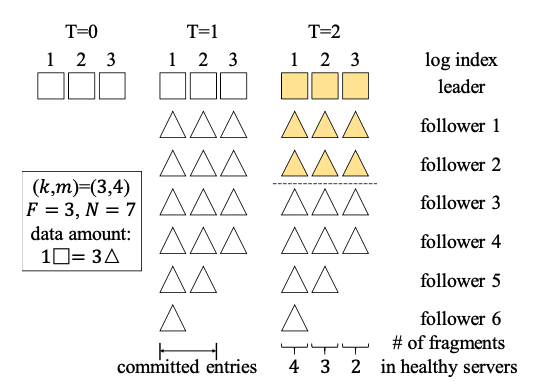
image-20230316145948620

2 * 3 + 1,七个节点，可以容忍三个节点的failure，（k，m） = （3，4），
即一个日志被code成3个fragment和4个parity，一共7个coded fragment，可以容忍4个fragment的丢失，至少需要3个fragment
才能恢复出完整的日志。
假设使用 3 + 1即 4个节点应答就commit，例如log3，在T2时刻，仅剩4个节点active，因为只有两个fragment，
因此无法恢复出完整的log。

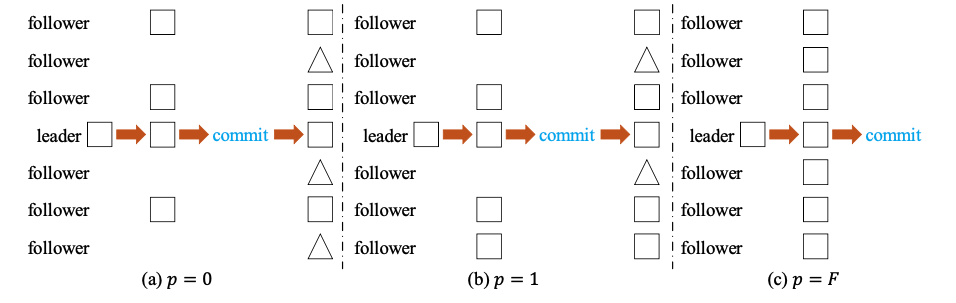
complete-entry replication

何时触发？

coded-fragment要求至少有F + k个节点存活，才能保证Liveness属性，因此如果Raft Group内的healthy节点个数在[F + 1, F + k)区间内时，需要转化为complete-entry replication。

日志提交条件

和经典raft一致，即日志得到F+1个slave的成功回复后，可以提交。

优化

在日志提交后，没有获取到日志的节点可以使用coded-fragment replication来节省Storage cost

定义参数p，0 ≤ p ≤ F，leader可以首先发送完整日志到F+p个followers，再向剩余的F-p个followers发送fragment。p值的大小和Storage&network cost成正比关系，当p = F时，退化成经典的raft算法。本文的实现中选取的p值为0。

image-20230316151703873

strategy prediction

算法

通过心跳信息来确定active Server的个数：

  1. 如果active Serve个数不少于F+k，触发coded-fragment replication
  2. 如果active Server个数少于F+k，触发complete-entry replication

image-20230316152248757

Newly-elected Leader

对于new elected leader，可能存在以下两种类型的日志：

  1. commit过的日志，coded-fragment replication 保证了至少有k个fragment可以恢复出此条日志，complete-entry replication保证了其他Server有存储过完整的日志，因此committed log可以在new elected leader上正确的恢复。
  2. unapply过的日志，没有机制可以保证此条日志可以正确的恢复，CRaft中引入了LeaderPre operation

LeaderPre operation

流程：
  1. new elected leader查找出本地unapplied code-fragments
  2. 为每条日志向所有的follower发送request
  3. 如果接收到了此条日志的完整副本或者k条fragment，则恢复出此条日志，但不会commit或者apply
  4. 如果无法恢复，删除
  5. 此过程中需要不断向slave发送心跳，防止触发新的选举

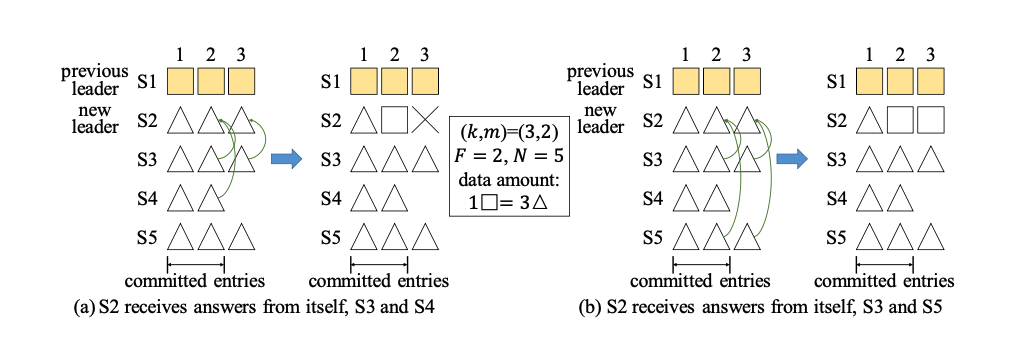
image-20230316154606324

unrecoverable意味着uncommitted，因此删除是harmless的。

具体证明

Leader Completeness Property：如果log e在term T被提交，那么e会在所有有更高term的leader中出现，且e不会被更高term中的leader删除。

反证：

假设LCP无法被hold，有两种场景：

  1. e在Term U的新Leader选举时不在Leader的日志中。
  2. e在Term U的新Leader选举的LeaderPre阶段中被删除了。

先证明场景1，根据假设，在Term T到Term U之间的所有Leader都持有log e且e没有被LeaderPre阶段删除过，因此e从Term T开始就没有被任何节点删除过。LeaderT将e至少分发给了F+1个节点，LeaderU至少接收到了F+1个节点的投票响应，根据排容原理，F+1 + F+1 = N + 1 > N,即至少一个节点接受了e日志且给LeaderU投了票。此Server先一定是先接受了e日志，再给LeaderU投票，否则，它会reject LeaderT的AppendEntris RPC。因为e从Term T开始就没有被删除过，且投票给了LeaderU，因此LeaderU的日志一定至少和此节点的日志一样新，因此LeaderU的日志中一定包含了e，这个假设1存在矛盾。（此证明和Raft经典论文的证明思路一致）

再证明场景2，假设在Term U中e被删除了，有一个无法被恢复的log e1，假设e1不是e，因为e被删除了，因此e1的index一定是小于e的。因为e在Term T中由LeaderT提交且e1的index小于e，因此e1也被提交过。因此e1打破了Leader Completeness Property且index比e小，因此此处矛盾，所以e1一定是e。(这边不是废话吗？论文里假设的就是e在Term U中被删除了)。所以e因为无法正确的恢复而在LeaderPre中被删除。因为e在Term T中被提交，所以至少完整的复制到了F+1个节点上或者以EC Fragment的形式被部分的复制到了至少F+k个节点上，因此e一定是能够被恢复的。此处和假设2产生矛盾。

Performance

Overview

  1. 新的Leader选出来后，需要做日志恢复，影响性能
  2. LeaderPre会延长选举时间，影响可用性
  3. 新选举的Leader恢复所有完整的日志带来的损耗和降低读延迟之间存在取舍
  4. 日志滞后的节点当前无法通过snapshot来同步，snapshot机制在CRaft中要复杂的多
  5. 编解码会消耗CPU

Latency

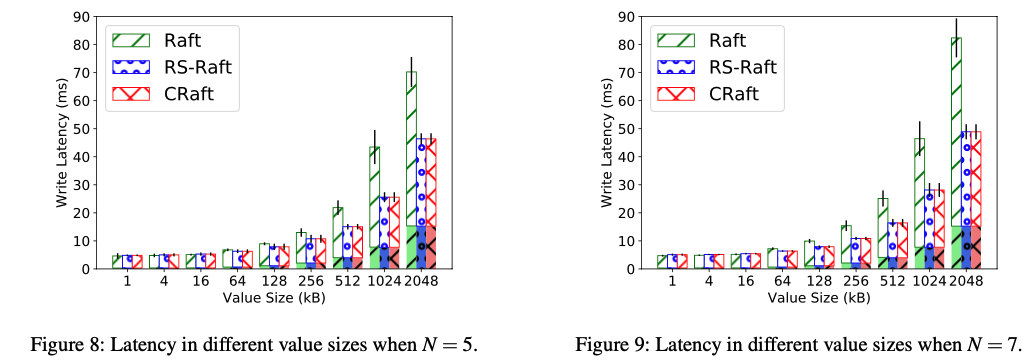
image-20230316162654905

在value size比较小的时候，几乎没有性能区别，在value size比较大的时候，因为CRaft只做coded-fragment分发，因此性能优势明显。（they reduce 20%–45% of latency compared to Raft when N = 5, and 20%–60.8% when N = 7.）

Throughput

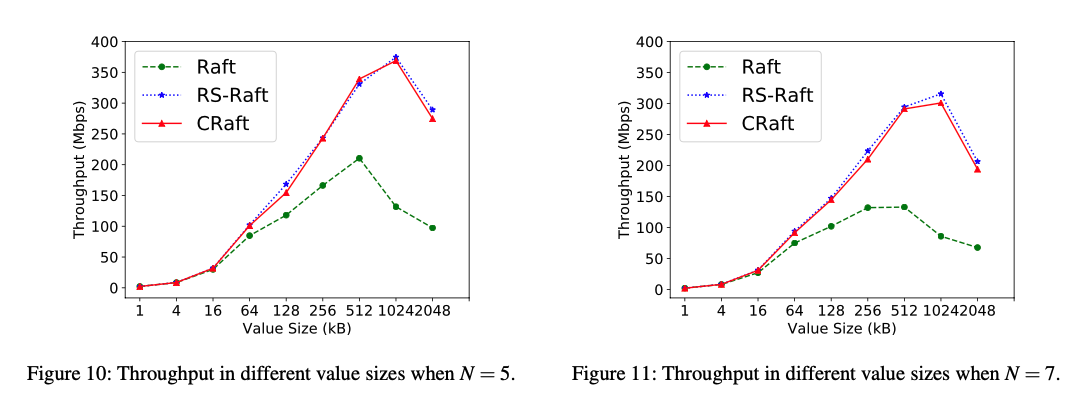
image-20230316163237975

value size比较大的时候，对于带宽的提升明显，大到临界点时，总带宽会降低，因为遇到了网络拥塞问题（CRaft and RS-Raft can have a 180% improvement on write throughput when N = 5 and 250% when N = 7. Also, the throughput peaks of CRaft and RS-Raft both appear much later than Raft’s. ）

Network Cost

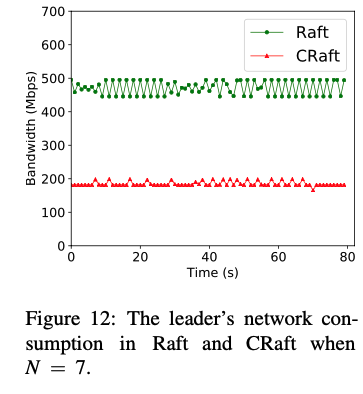
image-20230316164326189

通过leader端的检测，Craft相较于原始raft协议，在N = 7时，配置不同的k值，raft中leader的数据发送量是Craft的250%~300%

Liveness

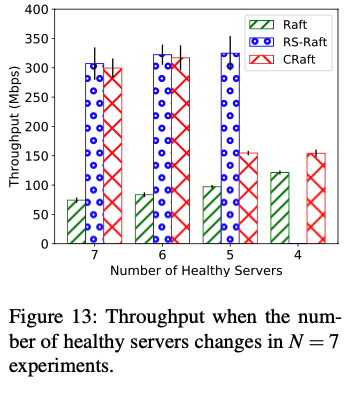
健康节点数为5时，CRaft的带宽不如Rs-Paxos,因为CRaft必须使用complete-log replication

健康节点数为4时，Rs-Paxos无法work。

节点数 CRaft可以容忍的失败节点数 RS-Paxos可以容忍的失败节点数
5 2 1
7 3 2

image-20230316164936694

Recovery Read

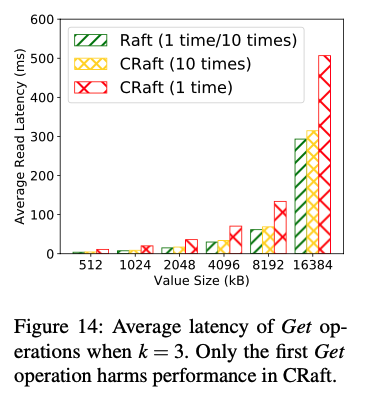
当leader发生切换时，在CRaft中，第一次读取可能需要leader做Recovery，因为leader可能只存储了log的部分fragment，假如leader不发生频繁切换，那么CRaft的read延时和Raft类似，在Recovery Read中，相较于Raft，延时为raft的1.4倍左右，当多次读同一个key时，延迟基本相当。

image-20230316165402693

Conclusion

Raft RS-Paxos CRaft
Storage cost 2F + 1 2F / k + 1 2F / k + 1
network cost 2F 2F / k 2F / k
liveness level F F - (k - 1) / 2 F
Commit slave reply cnt F + 1 F + 1 F + k

Q&A:

  1. m和k之间的约束是什么，在实际的工业场景中，此算法的价值如何？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
现有：m + k = N（1）

		2F + 1 = N（2）

需满足：F  + k < N (3)，即不需要commit_all

由（2）（3）可得：(N - 1) / 2 + k < N，可得k < ( N + 1) / 2 （4）

由（4）可得：m + k  < m + (N + 1) /2 （5）

由（1）（5）可得：N < m + (N + 1) /2，可得m > (N - 1) / 2 （6）

由（2）（6）可得：m > (2F + 1 - 1) / 2，可得m > F

因为m为整数，所以m至少为F+1。

当m为F + 1时，由（1）可得，k = F， 此时F + k = 2F，即在最坏的case，要2F个节点确认后才能提交log。
k m commit条件
F F + 1 2F
F - 1 F + 2 2F - 1
F - 2 F + 3 2F - 2
… … …
F - x F + x + 1 2F - x

2F - x >= F + 1,即 x <= F - 1。

k m commit条件
F + 1 F 2F + 1
F + 2 F - 1 2F + 2 (无法使用CRaft)
F + 3 F - 2 2F + 3 (无法使用CRaft)
… … …
F + x F + x + 1 2F - x (无法使用CRaft)

结论：

  1. 按照上面的推导，k比m小的越多，则commit的条件越宽松
  2. 在k大于m的场景中，k最小为F+1,m为F，此时F+k = 2F + 1 = N,为commit_all, k再大的话，不满足条件，无法使用CRaft
  3. 在实际的场景中，k往往比m大，因此CRaft的应用条件比较有限。